| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | ||||
| 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 11 | 12 | 13 | 14 | 15 | 16 | 17 |
| 18 | 19 | 20 | 21 | 22 | 23 | 24 |
| 25 | 26 | 27 | 28 | 29 | 30 | 31 |
- Object Detection
- Deeplearning
- point cloud
- 파이썬
- NLP
- 프로그래머스
- transformer
- 알고리즘
- Python
- 3D
- Object Tracking
- deep learning
- attention
- Computer Vision
- 자료구조
- re-identification
- Knowledge Distillation
- flame
- 스택
- 딥러닝
- 큐
- cv2
- 임계처리
- center loss
- level2
- numpy
- OpenCV
- reconstruction
- 논문 구현
- Threshold
- Today
- Total
공돌이 공룡의 서재
[논문 리뷰] Adversarial attack: Universal Adversarial Perturbation 본문
Universal Adversarial Perturbation
https://arxiv.org/abs/1610.08401
Adversarial attack. 이미지에 사람은 감지하기 힘든 작은 노이즈를 추가했을 때, 분류기의 성능이 확 낮아지는 것을 말한다.

이 논문에서는 딥러닝 모델 전체적으로 또는 데이터셋 전체적으로 적용되며 분류기가 제 기능을 못 하도록 하는 perturbation (감지하기 힘든 작은 노이즈라고 보면 될 듯)을 다룬다.
<1> Introduction

이미지에 quasi-imperceptible (감지하기 힘든) perturbation (사전 상 의미는 작은 변화인데, 노이즈 정도로 생각하면 될 듯)을 주었을 때, 신경망이 잘 못 분류할 가능성이 커질 수 있다는 문제를 제시한다.
이런 문제를 만드는 perturbation을 universal이라 하는데 이들 때문에 실제 상황에서 분류기의 성능에 문제가 될 수 있다. 분류기의 성능을 저하시키는 적(adversary)으로 쓰일 수 있기 때문이다.
이런 perturbation의 존재는 신경망의 decision boundary의 topology에 대해 새로운 insight를 제시한다.
이 논문의 main contribution은 다음과 같다.
- SOTA 신경망에 universal image-agnostic (이미지에 대한 지식 없이도 적용되는) perturbation의 존재를 보였다.
- 이런 perturbation을 찾는 알고리즘을 제시했다.
- universal perturbation은 놀랄만한 일반화 성능을 보였다. 새로운 이미지들을 높은 확률로 속이는게 가능했다.
- 이런 perturbation들은 이미지 전반에 걸쳐 universal할 뿐 아니라, 신경망에도 적용되었다. 즉, 데이터나 신경망 구조적 측면 둘 다에 universal 하다. (doubly universal)
- decision boundary의 다른 부분들 사이 geometric correlation을 사용해서 신경망이 universal perturbation에 얼마나 취약한지를 분석했다.
<2> Universal perturbations
perturbation에 대한 정의를 수식적으로 나타내고 있다. Introduction 끝 부분에 나와있기 하지만, 이전에 연구되었던 perturbation과는 다른 정의를 사용한다.
: 이미지의 분포로 부터 샘플 된 거의 모든 데이터 포인트에 대해 분류기를 속일 수 있는 어떠한 perturbation vector. (v)
$$ \hat{k}(x+v) \; \neq \hat {k}(x) \;\; for \;\; ``most" \; x \sim \mu $$
여기서 k는 분류기, x는 각 이미지, u는 이미지 분포를 뜻한다.
논문에서는 자연스러운 이미지를 포함해서 다양성이 매우 높은 distribution mu를 가정했을 때, 일정 비율 이상 속일 수 있고 특정 magnitude보다 작은 vector를 찾고자 했다.
[알고리즘]
image set X 의 data point에 대해 iteration 하면서 universal perturbation을 build 한다.
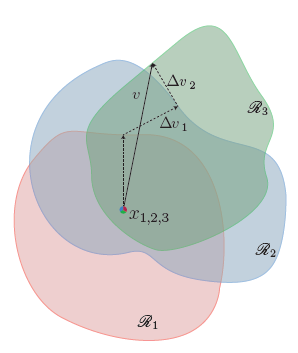

data point에 대해서 update 되는 과정을 도식화하면 위의 그림과 같고, 논문에서 제시된 알고리즘은 다음과 같다. 이 알고리즘은 가장 작은 벡터 v를 찾기보다는 충분히 작은 v를 찾는 과정이다.
딥러닝 모델 같은 standard classifier의 경우, 최적화 문제가 convex하지 않기 때문에, Deepfool 이란 논문에서 제시된 방법을 사용했다고 한다.
<3> Universal perturbations for deep nets

Imagenet validation set에 대해 알고리즘을 적용해서 찾은 universal perturbation을 적용하고, 얼마큼 속였는지를 나타낸 것이다. 비율이 매우 높았다. 이 실험으로, 사람은 감지하기 힘들지만 자연스러운 이미지를 잘 못 분류하게 만드는 single perturbation vector가 존재함을 보였다.

이때 같은 네트워크에 대해 universal perturbation들은 여러 개가 있을 수 있다는 점도 주목해야 한다. 패턴상으로는 비슷해 보이더라도, 내적 결과 유사도는 굉장히 낮았다. 이는 다양한 universal perturbation을 찾을 수 있음을 암시한다.
또 다른 실험을 진행해본 결과, universal perturbation을 찾는 데이터셋의 크기가 작아도 신경망을 속이는 것이 가능했다. 결과상 데이터셋이 크면 더 많이 속일 수 있었다. 또한 보이지 않는 데이터에 대해서도 일반화 성능을 보여줬다.
[Cross-model universality]

A라는 모델에서 찾은 universal perturbation이 B라는 모델에서도 잘 적용되는지를 찾는 문제다. 표에서 보듯이 모델이 달라져도 fooling rate가 높았다. 이는 알고리즘으로 찾은 perturbation이 데이터뿐 아니라 모델에도 적용되는, 즉 doubly universal 함을 의미한다.
[Visualization]

그래프 자료구조를 이용해서, perturbation의 영향을 시각화하였다. 그 결과, 위 그림처럼 일부 dominant 한 label들을 볼 수 있었다. 논문에서는 이런 label들은 image space에서 큰 영역을 차지하고 있다고 가설을 세운다.
[Fine tuning]
perturbation이 적용된 이미지들과 원본 이미지들을 섞어서, 모델을 fine-tuning 했다. 그 결과, 조금 나아지긴 했으나 큰 차이가 없었다. 다른 universal perturbation들도 섞어서 다시 fine-tuning 했으나 역시 마찬가지였다. (mild improvement만 있었다.)
<4> Explaining the vulnerability to universal perturbations
다른 다양한 perturbation과 비교를 해보는 실험을 했다. 대상은 random / adversarial over random samples / sum of adversarial perturbation over X / mean of images이다.

논문에서는 random과 universal의 큰 차이는, universal perturbation이 분류기의 decision boundary들 사이 어떠한 geometric correlation을 사용하고 있다고 제시한다.
알고리즘에서 사용한 방법에 의해서, adversarial perturbation vector r(x)는 decision boundary에 normal하다. 따라서 geometry에 대한 정보를 담고 있다고 할 수 있다.

decision boundary에 대한 normal vector들로 구성된 matrix를 정의하고, 이 matrix의 singular value의 변화를 확인했다. 다른 random 한 matrix랑 비교했을 때 decay 정도가 다른 것으로 보아, 신경망의 decision boundary들 사이에 큰 상관관계가 있다고 할 수 있다. 더 정확히는 normal vector 대부분을 포함하는 더 낮은 차원의 subpace가 있다고 할 수 있다. universal perturbation의 존재는 이러한 subspace가 있기 때문이라고 한다. 위에서 제시된 알고리즘은 결국 subspace에서 랜덤 하게 벡터를 고른다기보다는 fooling rate를 최대할 수 있도록 subspace 내에서 특정 방향을 고르는 것이라 할 수 있다.
'딥러닝' 카테고리의 다른 글
| [논문 리뷰] XNOR - Net : classification using Binary CNN (0) | 2021.09.14 |
|---|---|
| [개념] CNN : Convolution의 의미에 대하여 (0) | 2021.03.12 |
| [구현] 퍼셉트론 Numpy로만 구현하기 / Implement Perceptron by using Numpy Only (0) | 2021.01.02 |



