| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | |||
| 5 | 6 | 7 | 8 | 9 | 10 | 11 |
| 12 | 13 | 14 | 15 | 16 | 17 | 18 |
| 19 | 20 | 21 | 22 | 23 | 24 | 25 |
| 26 | 27 | 28 | 29 | 30 | 31 |
- 프로그래머스
- transformer
- Computer Vision
- flame
- Knowledge Distillation
- numpy
- reconstruction
- attention
- Deeplearning
- OpenCV
- deep learning
- 3D
- Object Detection
- 논문 구현
- Python
- 딥러닝
- 자료구조
- 알고리즘
- NLP
- 스택
- Threshold
- re-identification
- 큐
- cv2
- level2
- Object Tracking
- 파이썬
- center loss
- point cloud
- 임계처리
- Today
- Total
공돌이 공룡의 서재
CV :: [이론 / 구현] ICP algorithm : point to plane 본문
이번에 알아볼 ICP 알고리즘은
바로 전에 작성한 글 ICP point to point 방법과는 달리 normal vector를 사용한 방법이다.
구현한 논문은 다음과 같다.
https://www.comp.nus.edu.sg/~lowkl/publications/lowk_point-to-plane_icp_techrep.pdf
수식적으로 복잡한 부분이 많아서 과정을 코드와 함께 살펴보고자 한다.
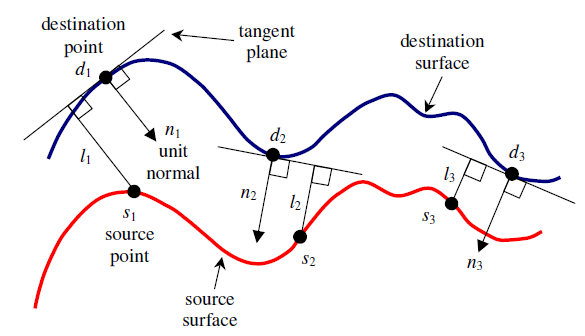
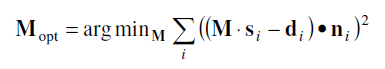
M은 최적화하고자 하는 4x4 transformation 식이다. s는 source point cloud의 각 점에 해당하고, d는 destination point cloud의 각 점에 해당한다. n은 d에서 normal vector다.
normal vector라 하면 그 점의 접면에 수직인 벡터를 의미한다. 그러면 필요한 것은 이 normal vector들을 계산하는 과정인데, d를 중심으로 이웃하는 다른 da, db가 있다고 가정한다면, d에서 da, db로 향하는 벡터들의 외적은 우리가 구하고자 하는 벡터로 볼 수 있을 것이다. 전제로는 d와 da, db가 굉장히 가까워야 한다.
여기서 이웃하는 점들은 scikit-learn 모델 중에서 KDTree를 이용했다. normal vector들을 구하는 식은 다음과 같다.
# from sklearn.neighbors import KDTree
def normal_vector_set(pc):
tree = KDTree(pc, leaf_size=2)
dist, ind = tree.query(pc, k=3)
n_vectors = []
for i in range(len(pc)):
v1 = pc[ind[i, 1]] - pc[i]
v2 = pc[ind[i, 2]] - pc[i]
n = np.cross(v1, v2)
n_vectors.append(n)
return np.array(n_vectors)
그러고 나서, corresponding points들을 찾는 과정을 KDTree로 해결했다. 추후에 이전 포스트에서 사용했던 방법으로도 시도해보고자 한다. KDTree는 source point cloud로 tree를 만들어놓고, query로 destination point cloud를 입력하면, source와 destination 각 점들에 대해서 가장 가까이 위치한 점들끼리 그 거리와 인덱스를 뽑아준다.
def nearest_neighbor(src, dst):
tree = KDTree(src, leaf_size=2)
dist, ind = tree.query(dst, k=1)
src_neighbored = src[ind].reshape(-1, 3)
return src_neighbored, dist
그러고 나서, 논문에 사용한 알고리즘 자체를 numpy로만 구현해보았다. 사실, 이렇게 구현하지 않고 open3d나 pcl에 있는 method를 불러와서 사용해보는 것이 더 효율적이긴 하다. 공부 차원에서 구현해보았다.
넘어가기 전에, 식(1)에 있는 M은 approximation을 통해 linear하게 다음과 같이 구성한다. 논문 제목에서 linear가 들어가는 이유기도 하다. 실제로는 좀 더 nonlinear하지 않을까 싶다. (논문이 옛날에 나오긴 했다.)
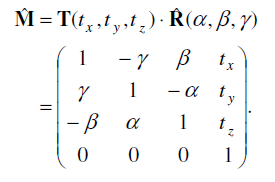
여기서 식(1)을 linear한 성격 때문에 조금의 전개를 거치고 나면 Ax-b 형태로 치환할 수 있다. 여기서 b는 아래와 같고
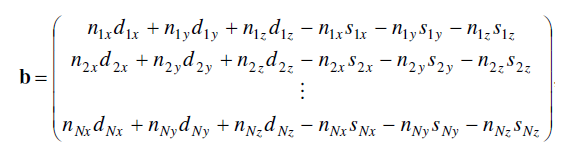
A의 경우 다음과 같다.
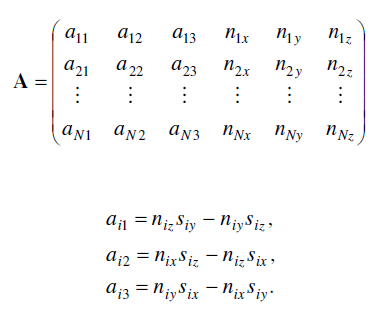
우리는 결국 식(1)을 위의 Ax-b의 제곱값이 최소가 되도록 하는 x를 찾고 싶은 것이다. 이때, x는 M의 parameter들, 즉 알파 감마 베타와 translation 값들을 의미하는 6x1 벡터다.
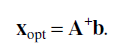
이때, linearity 때문에 SVD를 통해서 A의 pseudo-inverse를 구해주면 위와 같이 바로 값을 구할 수 있다. 이를 코드로 구현해보면 다음과 같다. 주석 처리한 부분은 논문에서 나온 내용을 있는 그대로 (더 raw 하게) 작성해본 것인데 남겨둔 식으로 더 간단하게 해결이 가능하기 때문에 사용하지 않았다.
def point2plane(src, dst, norms):
N = src.shape[0]
matrix_b = np.zeros((N, 1))
for i in range(N):
matrix_b[i] += norms[i, 0]*dst[i, 0] + norms[i, 1]*dst[i, 1] + norms[i, 2]*dst[i, 2]
matrix_b[i] -= norms[i, 0]*src[i, 0] + norms[i, 1]*src[i, 1] + norms[i, 2]*dst[i, 2]
matrix_A = np.zeros((N, 6))
matrix_A[:, 3:] = norms
for i in range(N):
matrix_A[i, :3] = np.cross(src[i], norms[i])
# matrix_A[i, 0] = norms[i, 2]*src[i, 1] - norms[i, 1]*src[i, 2]
# matrix_A[i, 1] = norms[i, 0]*src[i, 2] - norms[i, 2]*src[i, 0]
# matrix_A[i, 2] = norms[i, 1]*src[i, 0] - norms[i, 0]*src[i, 1]
# U, S, Vt = np.linalg.svd(matrix_A, full_matrices=False)
# S_inv = np.zeros((U.shape[1], Vt.shape[0]))
# for i in range(len(S)):
# S_inv[i, i] = S[i]
# S_inv = np.linalg.inv(S_inv)
# matrix_A_inv = Vt.T.dot(S_inv).dot(U.T)
matrix_A_inv = np.linalg.pinv(matrix_A)
x_opt = matrix_A_inv.dot(matrix_b) # alpha, beta ,gamma, tx, ty, tz
M = np.eye(4)
M[0, 1] = -x_opt[2]
M[0, 2] = x_opt[1]
M[0, 3] = x_opt[3]
M[1, 0] = x_opt[2]
M[1, 2] = -x_opt[0]
M[1, 3] = x_opt[4]
M[2, 0] = -x_opt[1]
M[2, 1] = x_opt[0]
M[2, 3] = x_opt[3]
return M
그래서 최종적인 ICP algorithm은 다음과 같다.
입력으로 들어오는 src와 dst는 Nx3 형태의 point cloud 여야 한다.
def icp(src, dst, tolerance=1e-7):
m = src.shape[1]
assert m == 3
N = min(src.shape[0], dst.shape[0])
sampler = random.sample(range(N), N)
source = np.ones((m+1, N))
tar = np.ones((m+1, N))
source[:m, :] = np.copy(src[sampler, :].T)
tar[:m, :] = np.copy(dst[sampler, :].T)
prev_error = 0
count = 0
M = np.eye(4)
while True:
src, dist = nearest_neighbor(src, dst)
norms = normal_vector_set(dst)
T = point2plane(src, dst, norms) # T = 4x4
mean_error = np.mean(dist)
if np.abs(prev_error - mean_error) < tolerance:
print('Iterate loop:: ', count)
break
source = T.dot(source)
M = M.dot(T)
src = source[:3, :].T
prev_error = mean_error
print(prev_error)
count += 1
return src, M
normal vector를 이용한 방법을 사용하면 더 빠르다고 들었는데 구현한 코드에서는 low-level 단계에서 작성해서 그런지 시간은 좀 오래걸렸다. 결과는 다음과 같다. 초록색이 이동시킨 source, 빨간색이 target에 해당한다.
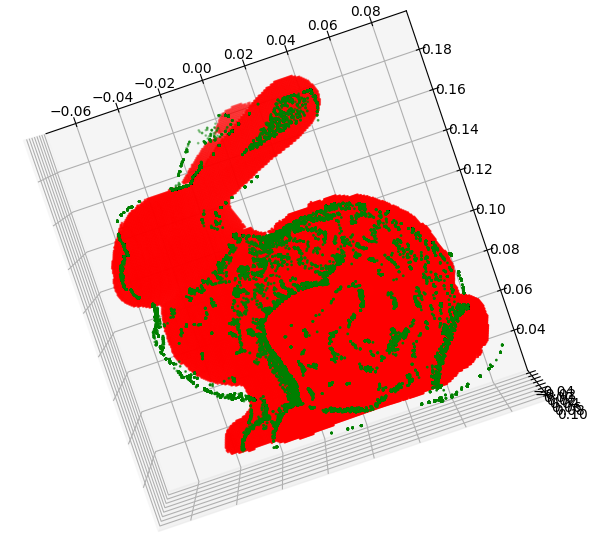
Iteration 자체는 24번으로 point-to-point와 비교했을 때 훨씬 적었으나, 벡터나 numpy 계산이 많다보니 시간 자체는 더 오래 걸렸다. 200초 정도 나온 것 같다. 개선할 여지는 좀 더 있을 것 같은데, 여유가 되면 해보고 우선은 SLAM 쪽으로 리뷰하고자 한다.
Full code : https://github.com/minsu1206/3D/blob/main/ICP/point-to-plane.py
'컴퓨터비전' 카테고리의 다른 글
| CV :: [이론 / 구현] ICP algorithm : point-to-point (0) | 2021.08.26 |
|---|

