| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | ||||||
| 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 9 | 10 | 11 | 12 | 13 | 14 | 15 |
| 16 | 17 | 18 | 19 | 20 | 21 | 22 |
| 23 | 24 | 25 | 26 | 27 | 28 |
- attention
- Python
- deep learning
- 3D
- numpy
- Knowledge Distillation
- 스택
- 파이썬
- center loss
- 논문 구현
- level2
- NLP
- 딥러닝
- 임계처리
- 알고리즘
- cv2
- flame
- Computer Vision
- point cloud
- reconstruction
- re-identification
- Object Tracking
- 자료구조
- Object Detection
- 프로그래머스
- transformer
- 큐
- Deeplearning
- Threshold
- OpenCV
- Today
- Total
공돌이 공룡의 서재
CV :: [이론 / 구현] ICP algorithm : point-to-point 본문
ICP: Iterative Closest Point

이 알고리즘은 두 개의 point cloud가 주어졌을 때, corresponding point 사이의 거리를 계산하여, 이 거리를 최소화하는 Transformation matrix을 찾는 알고리즘이다.
이 알고리즘을 공부하게 된 계기는 depth camera에서 reconstructed 된 point 들을 통해 camera간 pose를 계산하기 위함이었다.
corresponding point를 찾는 알고리즘은 KDTree 등 여러 알고리즘이 있지만, 이건 다음에 살펴보고, 여기선 corresponding point들이 주어졌다는 가정하에 ICP 알고리즘에 대해서만 알아보겠다.
크게 point-to-point 방법과 point-to-plane 방법이 있다.
point-to-plane
1.
target point cloud를 X라 두고, 여기에 속하는 포인트를 x라 하자. transformation 시키고 싶은 point cloud를 source point cloud라 하고, 여기서 속하는 포인트를 p라 하자.
각 point cloud의 평균 3D 좌표를 구한 다음에, 각 point cloud 안에 속하는 모든 점들에 대해 이를 빼주면 중심이 (0,0,0)으로 이동된다.
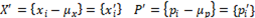

2.
$$ W = \sum_{i=1}^{N_p}x_i'p_i^T $$
그다음, 각 correspondence point들끼리 곱한다. 이때 만들어지는 matrix W는 3x3 matrix다. 이때, SVD를 이용하면 이 matrix W를 다음과 같이 나타낼 수 있다.
$$ W = U\Sigma V^T $$
3.
여기서 구해진 U, V를 이용하여 R, T를 구할 수 있다. 정의는 다음과 같다.
$$ R = UV^T $$
$$ t = \mu_x - R\mu_p $$
4.
얻고자 하는 R, t는 다음 식을 최소화하는 값들이다. least-square 방법을 이용한다.
$$ E(R, t) = \frac {1}{N_p}\sum_{i=1}^{N_p} \parallel x_i - Rp_i - t \parallel^2 $$
5.
이 R, t를 source point cloud에 적용시킨다. 그러고 나서, 다시 1번으로 돌아간다. 오차가 수렴할 때까지 이를 반복한다.
[내용 추가] http://www5.informatik.uni-erlangen.de/Forschung/Publikationen/2005/Zinsser05-PSR.pdf
Scaling factor를 이용한 point-to-point를 사용하니 더 좋은 결과를 얻을 수 있었다.


그러고 나서, $$ t = \mu_x - sR\mu_p $$ 이렇게 정의한다. Iterative 방법은 위와 동일하다.
코드 구현은 scaling factor를 추가하여, 아래와 같이 하였다.
https://github.com/minsu1206/3D/blob/main/ICP/point-to-point.py
결과는 다음과 같았다.
주의해야 할 점은 source point cloud와 target point cloud 간 개수가 같아야 해서, 다르다면 더 적은 쪽의 수를 기준으로 두고 random 하게 점들을 sampling 하는 방식을 선택했다.

수렴 조건을 현재 error와 이전 error 간 차이를 1e-7로 주었더니 104번 iteration 하고 mean error가 0.00155 정도 나왔고, 1e-8 이하부터는 error가 비슷했다. 결과 자체도 육안으로 구분하기 힘들었다. 충분히 수렴했다고 볼 수 있다. 시간은 1e-7로 두고 했을 때, 59.1초가 나왔다.
'컴퓨터비전' 카테고리의 다른 글
| CV :: [이론 / 구현] ICP algorithm : point to plane (0) | 2021.08.27 |
|---|

