| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | ||||
| 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 11 | 12 | 13 | 14 | 15 | 16 | 17 |
| 18 | 19 | 20 | 21 | 22 | 23 | 24 |
| 25 | 26 | 27 | 28 | 29 | 30 | 31 |
- transformer
- NLP
- reconstruction
- re-identification
- 딥러닝
- 프로그래머스
- Deeplearning
- cv2
- Python
- point cloud
- Object Detection
- 자료구조
- attention
- deep learning
- center loss
- 3D
- Knowledge Distillation
- Threshold
- level2
- flame
- 파이썬
- numpy
- 알고리즘
- 스택
- OpenCV
- 임계처리
- Object Tracking
- Computer Vision
- 큐
- 논문 구현
- Today
- Total
공돌이 공룡의 서재
[python openCV] 이미지 처리 - 임계 처리 (3): triangle algorithm thresholding 논문 분석 및 구현 본문
[python openCV] 이미지 처리 - 임계 처리 (3): triangle algorithm thresholding 논문 분석 및 구현
구름위의공룡 2020. 9. 11. 23:110. 들어가기 전
2020/09/02 - [코딩/opencv] - [python openCV] 이미지 처리 - 임계 처리 (1): inRange, threshold
첫 번째 임계처리 포스트에서 otsu와 triangle에 대해 알아보았고, 두 번째 포스트에서는 otsu를 deep하게 알아보았다. 이번 포스트에선 마지막으로 triangle algorithm을 자세히 다루고자 한다.
이 thresholding은 정보면에서 조금 문제가 있었기에 목차는 다음과 같이 하여 작성하겠다.
- 논문 설명
- 알고리즘
- 코드 구현 (1) & 문제 상황
- 코드 구현 (2) & 해결 방법
핵심만 알고 싶은 분은 3번째 목차는 생략해도 상관없다.
1. 논문
(1) 원본
링크: journals.sagepub.com/doi/pdf/10.1177/25.7.70454
논문 제목:
Zack, G. W., Rogers, W. E. and Latt, S. A., 1977, Automatic Measurement of Sister Chromatid Exchange Frequency, Journal of Histochemistry and Cytochemistry 25 (7), pp. 741-753
(2) 설명
안타깝게도 threshoding에 대한 구체적인 내용은 존재하지 않는다. 논문 제목에서부터 알 수 있다시피 원래 이 논문의 목적은 sister chromatid, 자매 염색분체 관찰에 대한 내용이 주다. 그래서 이 염색분체의 특성과 관찰결과로 얻은 distribuition에 대한 논의를 메인으로 다룬다.

논문에서 나온 thresholding 방법에 관한 내용은 이게 전부다. 구글링을 해도 비슷한 내용만 나올 뿐 결과를 확인하기 힘들었는데 해결 과정에서 겪은 문제 상황과 내가 세웠던 가설을 바탕으로 알고리즘 내용을 풀어보겠다.
2. 알고리즘
1) 배경
이 thresholding 방법이 나오게 된 배경이 뭘까? 우선 이것부터 알아보자. 그러면 알고리즘이 어떻게 진행되는지 이해하기가 수월할 것이다.
이전 포스트 otsu algorithm paper를 다룰 때에도 처리 알고리즘의 목적은 background와 object를 구분하는 것이다. 학교 다닐 시절에 과학시간에 현미경으로 세포막같은 것을 관찰해본 경험이 있을 것이다. 그때 빛을 이용하기 때문에 배경은 매우 밝고, 관찰 대상은 어둡게 보이게 된다. 그래서 비교적 크기가 큰 (마이크로미터 기준) 대상은 형태가 잘 보이는 반면 더 작은 대상들은 관찰하기 힘들다.
논문에서는 바로 이 포인트가 이 thresholding 방법을 쓰는 이유라고 설명하고 있다. 밝은 배경이 화면의 대부분을 차지하는 상황에서 작고 어두운 대상들을 더 뚜렷하게 관찰하려면 다른 방법이 필요하다는 것이다. 이 상황은 pixel intensity histogram에서 생각해볼 때, 위의 Fig.2 그림처럼 흰색에 가까운 값들의 빈도수가 많고 정작 관측하고자 하는 대상의 픽셀 값의 빈도수들은 작다. 이 같이 low peak level을 갖는 object와 high peak & many # 를 갖는 background를 구분할 때 용이한 방법이라 할 수 있겠다.
2) 알고리즘(방법)
- 히스토그램에서 가장 빈도수가 높은, 즉 peak가 되는 픽셀값을 찾는다. 그 픽셀값에서 가장 먼 끝 값을 찾는다(farthest end). 편의상 이를 end라 하겠다.
ex) 만약 150이란 값이 peak라면 0이 end. 60이 peak값이라면 255가 end가 되는 것이다. - peak ~ end 에 해당하는 구간만 따진다. 이 구간에 대해 normalize를 한다. 한글말로 해서 표준화, 또는 정규화를 한다는건데 Fig.2처럼 가로 세로 비율을 1:1로 만들어준다는 것이다 (★)
- peak 부터 end까지 iteration하면서 d값이 최대가 되는 지점을 찾는다.
- offset을 고려하여 경계값을 조절한다.
이제 여기서 방법에 대해 그림과 수식으로 조금 더 살펴보자.

자 우선은 이렇게 픽셀 히스토그램을 2D 좌표평면으로 옮겨서 생각해보자. 위에 올린 Fig2의 white와 black은 무시하고 편하게 x축 기준, 오른쪽으로 갈수록 밝아지고 왼쪽으로 갈수록 어두워진다 생각하자. peak의 x좌표를 원점으로 놓는다면 peak와 end를 각각 좌표로 위와 같이 설정할 수 있을 것이다. 이제 ROI (region of interest)를 0부터 end로 놓고 생각해보자. 참고로 peak의 값이 128보다 큰 경우는 end와 peak자리가 바뀐 상태로 진행하면 된다.
peak부터 end까지를 1로 만들었는데 왜 1로 두지 않고 end로 두지? 라는 의문점이 생길 수 있다. y축 범위와 x축 범위의 값이 1이여야만 하는 것이 아니라 둘이 같은 비율이면 되는 것이다. 즉, x축의 범위가 75부터 255까지라면, y 값에 해당하는 픽셀 빈도수들을 모두 180으로 나누어도 충분하다. x축 범위까지 나누는 불필요한 계산을 없애기 위함이다.
위의 그림을 보면
$$ d = h \cdot sin(\beta) $$
가 성립함을 알 수 있을 것이다. 여기서 하나 더. 이 beta 값은 모든 x값. 즉 픽셀 값에 대하여 고정이다. 직선에서 x축 방향으로 내린 수선은 서로 평행하기 때문이다.
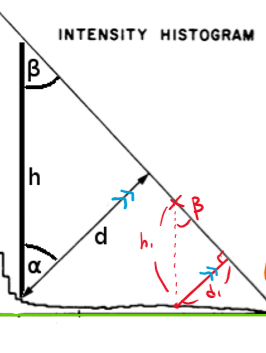
그럼 우선은 h를 구하든 beta값을 구하든 저 직선에 대한 식을 구해야 함을 의미하는데 peak와 end 두 지점의 좌표를 알고 있으므로 직선 식을 구할 수 있다.
$$ y = mx +c $$
이라 놓고 이 두 직선이 peak와 end를 지나므로,
$$ y - f(0) = m(x - 0) $$
$$ y - f(end) = m(x - end) $$
두 식이 성립함을 알 수 있다.
어떤 픽셀 값 i 에 대한 h는 다음과 같이 나타낼 수 있다.
$$ h_i = m \cdot i + c - f(i) $$
sin(beta) 값이야 m 값을 구하고 나면 삼각함수 식을 이용해서 변형시키면 나온다.
$$ sin(\beta) = \sqrt \frac{1}{m^2+1} $$
따라서 어떤 픽셀 값 i 에 대한 d는 다음과 같이 나타낼 수 있다.
$$ d_i = h_i \cdot sin(beta) = h_i \cdot \sqrt \frac{1}{m^2+1} $$
직선과 삼각함수만 안다면 쉽게 이해할 수 있는 굉장히 직관적인 방법이라 할 수 있겠다.
3. 코드 구현 (1) & 문제 상황
(1) 계산 간소화
sin(beta)와 c 값은 모든 d_i에 공통으로 들어가는 계산이다. 따라서 실제로 threshold를 찾을 때에는 이 과정을 생략하고
$$ m \cdot i - f(i) $$
값의 비교를 통해서 찾는 것이 가능하다. 음수 값이 나온다면 c값을 포함시키지 않아서 그런것이니 상관없다. 무조건 큰 값이면 되니까 사실 음수가 나온 순간 후보에서 이미 탈락.
(2) 코드 및 문제 상황
import cv2
import time
import numpy as np
import matplotlib.pyplot as plt
road = cv2.imread('./road.jpg')
gray = cv2.cvtColor(road, cv2.COLOR_BGR2GRAY)
height, width = gray.shape
hist = cv2.calcHist([gray], [0], None, [256], [0,256])
data = hist.flatten()
class Old_triangle:
def __init__(self, histogram):
self.hist = histogram
self.angle = 0
self.d = 0
self.top = 0
self.m = 0
self.const = 0
self.where = 0
def normalize(self):
"""
step1. find roi(=region of interest)
roi is btw pixel peak and farthest end from peak.
step2. normalize roi
the ratio of width / height should be 1.
so divide histogram value by number of roi pixel values
step2-2. y val of end value should be 0.
step2-3. When considering offset, index can be moved +- 1 according to x_peak >= 128 or not.
"""
self.top = np.argmax(self.hist)
roi = None
print('top', self.top)
if self.top >= 128:
roi = self.hist[:self.top+1]
low = np.min(roi)
roi = np.subtract(roi, low)
roi = np.divide(roi, len(roi))
end_xy = [0, roi[0]]
peak_xy = [len(roi) - 1, roi[len(roi)-1]]
self.where = -1
# end_xy = [len(roi) - 1, roi[len(roi) - 1]]
else:
roi = self.hist[self.top:]
low = np.min(roi)
roi = np.subtract(roi, low)
roi = np.divide(roi, len(roi))
end_xy = [len(roi)-1, roi[len(roi)-1]]
self.where = 1
peak_xy = [0, roi[0]]
print(np.mean(roi) * len(roi))
print(np.mean(hist))
print(roi, end_xy, peak_xy)
return roi, end_xy, peak_xy
def find_d_max(self, roi, end_xy, peak_xy):
"""
step3. find linear equation y = mx + b which contains end_xy and peak_xy
step4. d = h * sin(beta). sin(beta) is constant, so not necessary
Assume P(x1, hist[x1]). h = m * x1 + b - hist[x1] where x1 = {0, 1, ... len(roi)-1}
actually, + b is also not necessary
"""
slope = np.round((peak_xy[1] - end_xy[1]) / (peak_xy[0] - end_xy[0]), 3)
# const = np.round(peak_xy[1] - slope * peak_xy[0], 3)
d_list = np.subtract(np.multiply(slope, np.arange(len(roi))), roi)
print(slope)
print(np.argmax(d_list), self.top)
self.where += np.argmax(d_list)
if self.top < 128:
self.where += self.top
self.d = np.max(d_list)
return self.where
def process(self):
region, p1, p2 = self.normalize()
threshold = self.find_d_max(region, p1, p2)
print(threshold)
def show_result(self):
plt.plot(self.hist)
plt.scatter(self.where, self.hist[self.where], s=50, c='r')
plt.annotate('optimal k: '+str(self.where), xy=(self.where, self.hist[self.where]), xytext=(self.where, 0),
arrowprops={'color': 'red'})
plt.show()
ret, binary = cv2.threshold(gray, self.where, 255, cv2.THRESH_BINARY)
cv2.imshow('result', binary)
cv2.waitKey()
old = Old_triangle(data)
old.process()
old.show_result()
코드의 이해를 돕자면, 결과인 threshold 값은 where에 저장된다. normalize는 표준화 작업을, process에서는 threshold값을 찾는 과정을 실행한다.
문제상황 1.
위의 결과로 실행했을 때, opencv의 코드와 1씩 차이가 나는 경우가 있었다.
이 문제는 step2-3으로 해결할 수 있었다. 정확한 이유는 잘 모르겠으나, offset을 고려한 과정이지 않을까... 싶다. peak의 위치가 128 이전, 예를 들어 60이라면 threshold는 60 과 255사이에서 나올텐데 결과로 나온 픽셀값에 +1을 해준다. 반대로 128 이상의 값에서 peak가 나온다면, 예를 들어 180이라면 threshold는 0과 180 사이에서 나올텐데 결과로 나온 픽셀값에 -1을 해준다. 이렇게 했을 경우 이 차이를 해결할 수 있었다.
문제상황 2.
다른 그림으로 실행했을 때 완전 생뚱맞은 threshold가 구해지는 경우가 있었다.

이 사진으로 실행했을 경우, opencv를 이용했을 때는 50이 나왔는데 구현한 코드로는 107이라는 엉뚱한 결과가 나왔다.

이 사진을 이용했을 경우엔 opencv로는 100, 구현한 코드로는 146이 나왔다.
4. 코드 구현 (2) & 문제 해결
(1) 가설
원인이 뭐였을까. 우선은 pixel histogram을 plot하여 무엇이 잘못되었는지를 생각해보았다.
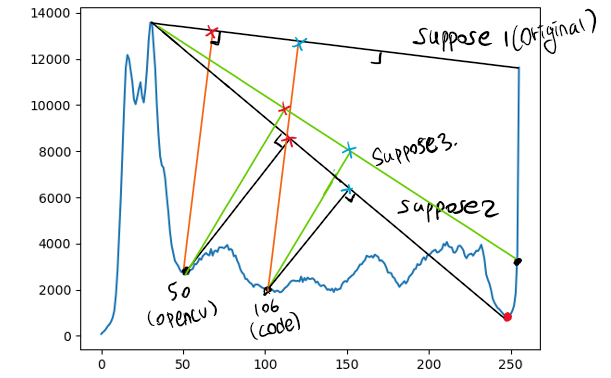
suppose1: 원래 방법대로 따른 경우다. 실제로 106일 때가 거리가 더 최대였다.
suppose2: 알고리즘의 의도를 생각했을 때 end가 빈도수가 매우 높은 값이라면 의도에 어긋난다 생각해서 end쪽의 local minimum으로 잡아야 하나 생각했다.
suppose3: 역시 의도를 생각하여 이미지 전체의 픽셀 빈도수 평균보다 높으면 end를 한칸 옮기는 방법을 생각했다. (초록선)

suppose4: 설마 end는 무조건 픽셀이 최솟값인 지점으로 해야하나 생각했다.
suppose5: end의 y값은 무조건 0으로 해야하나 생각했다.
많은 시행착오 끝에, 결과적으로는 suppose5의 방법이 필요했다. 다시 말하면, normalize를 다시 구현해야했다. ROI의 최소값을 ROI의 모든 y값에서 빼버리고, x축 범위의 길이와 같게 1:1로 맞춰 준 다음, end의 y값은 무조건 0으로 바꿔주었다. 그랬더니 opencv와 같은 결과를 얻을 수 있었다. 수정된 코드는 다음과 같다.
(2) 코드
import cv2
import time
import numpy as np
import matplotlib.pyplot as plt
road = cv2.imread('./cat.jpg')
gray = cv2.cvtColor(road, cv2.COLOR_BGR2GRAY)
height, width = gray.shape
hist = cv2.calcHist([gray], [0], None, [256], [0,256])
data = hist.flatten()
class Triangle:
def __init__(self, histogram):
self.hist = histogram
self.angle = 0
self.d = 0
self.top = 0
self.m = 0
self.const = 0
self.where = 0
def normalize(self):
"""
step1. find roi(=region of interest)
roi is btw pixel peak and farthest end from peak.
step2. normalize roi
the ratio of width / height should be 1.
so divide histogram value by number of roi pixel values
"""
self.top = np.argmax(self.hist)
roi = None
print('top', self.top)
if self.top >= 128:
roi = self.hist[:self.top+1]
low = np.min(roi)
roi = np.subtract(roi, low)
roi = np.divide(roi, len(roi))
end_xy = [0, 0]
peak_xy = [len(roi) - 1, roi[len(roi)-1]]
self.where = -1
# end_xy = [len(roi) - 1, roi[len(roi) - 1]]
else:
roi = self.hist[self.top:]
low = np.min(roi)
roi = np.subtract(roi, low)
roi = np.divide(roi, len(roi))
# end_xy = [0, roi[0]]
end_xy = [len(roi)-1, 0]
self.where = 1
peak_xy = [0, roi[0]]
print(np.mean(roi) * len(roi))
print(np.mean(hist))
print(roi, end_xy, peak_xy)
return roi, end_xy, peak_xy
def find_d_max(self, roi, end_xy, peak_xy):
"""
step3. find linear equation y = mx + b which contains end_xy and peak_xy
step4. d = h * sin(beta). sin(beta) is constant, so just h is needed.
Assume P(x1, hist[x1]). h = m * x1 + b - hist[x1] where x1 = {0, 1, ... len(roi)-1}
"""
slope = np.round((peak_xy[1] - end_xy[1]) / (peak_xy[0] - end_xy[0]), 3)
const = np.round(peak_xy[1] - slope * peak_xy[0], 3)
d_list = np.subtract(np.multiply(slope, np.arange(len(roi))), roi)
print(slope, const)
print(np.argmax(d_list), self.top)
self.where += np.argmax(d_list)
if self.top < 128:
self.where += self.top
self.d = np.max(d_list)
return self.where
def process(self):
region, p1, p2 = self.normalize()
threshold = self.find_d_max(region, p1, p2)
print(threshold)
def show_result(self):
plt.plot(self.hist)
plt.scatter(self.where, self.hist[self.where], s=50, c='r')
plt.annotate('optimal k: '+str(self.where), xy=(self.where, self.hist[self.where]), xytext=(self.where, 0),
arrowprops={'color': 'red'})
plt.show()
ret, binary = cv2.threshold(gray, self.where, 255, cv2.THRESH_BINARY)
cv2.imshow('result', binary)
cv2.waitKey()
tri = Triangle(data)
start = time.perf_counter()
tri.process()
finish = time.perf_counter()
print(finish - start)
tri.show_result()
위 코드로 실행 시 opencv로 처리했을 때와 같은 결과를 얻을 수 있었다.
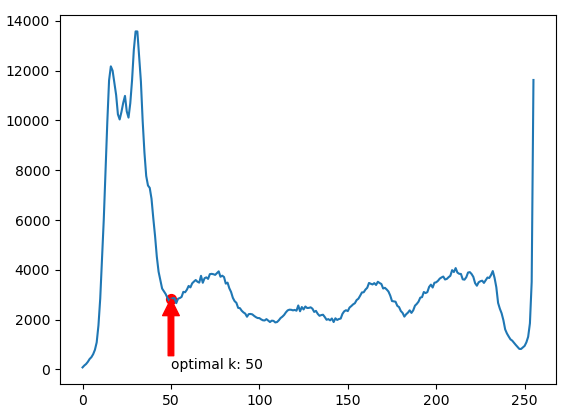

otsu는 정확한 수식과 방법들이 나와있어서 내용은 어려웠어도 구현할 때는 어려움이 없었는데 이 방법은 정보가 없어서 고생했다. 사실 왜 end의 값을 무조건 0으로 맞춰야 하는지 정확한 이유는 모르겠다.
아마 low level peak를 갖는 object니까 end의 값을 0으로 맞추는게 타당했을지도 모르겠다. 이 방법때문에 사진마다 object와 background의 처리 성능이 달라지겠다. 원래 의도대로인 밝은 배경에 어두운 물체에 대한 처리라면 효과적이겠다.
'코딩 > opencv' 카테고리의 다른 글
| [python openCV] 이미지 처리 - Canny Edge Detector (+Gaussian Filter) (1) | 2020.12.27 |
|---|---|
| [python openCV] 이미지 처리 - 임계 처리 (4): adaptive threshold (0) | 2020.09.22 |
| [python openCV] 이미지 처리 - 임계 처리 (2): otsu algorithm thresholding 논문 분석 및 구현 (0) | 2020.09.11 |
| [python openCV] 이미지 처리 - 임계 처리 (1): inRange, threshold (0) | 2020.09.02 |
| [python openCV] 이미지 처리 - 크기 / 색상 변환 : resize, cvtColor (0) | 2020.08.21 |




